DALL·E 1#
Blog post: https://openai.com/blog/dall-e/
Code: openai/dall-e (it’s not complete and covers only the dVAE part)
Model: Not available
Alternative code (PyTorch): lucidrains/DALLE-pytorch
Alternative code (JAX/Flax): borisdayma/dalle-mini

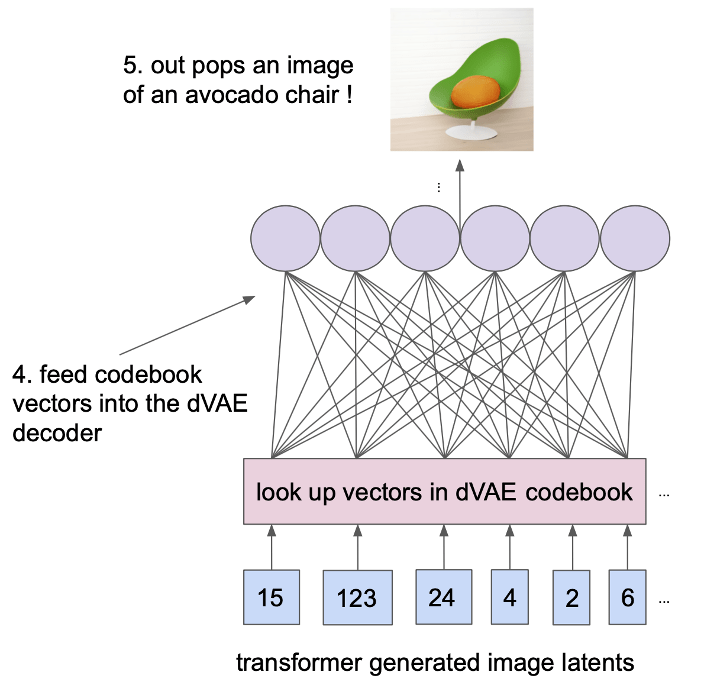
The first version of DALL·E was a GPT-3 style transformer decoder that autoregressively generated a 256×256 image based on textual input and an optional beginning of the image.
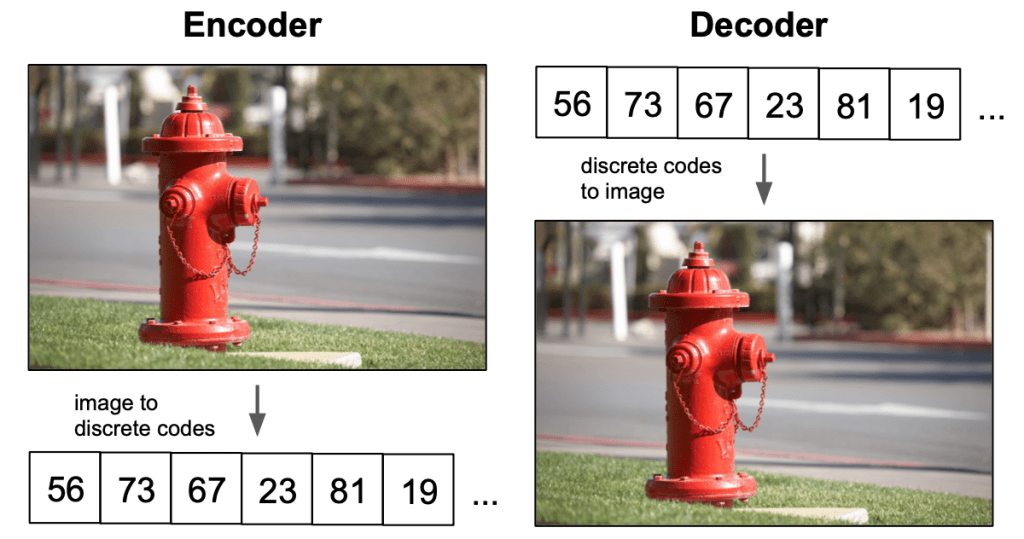
A text is encoded by BPE-tokens (max. 256), and an image is encoded by special image tokens (1024 of them) produced by a discrete variational autoencoder (dVAE).
dVAE encodes a 256×256 image into a grid of 32×32 tokens with a vocabulary of 8192 possible values.
Because of the dVAE, some details and high-frequency features are lost in generated images, so some blurriness and smoothness are the features of the DALL·E-generated images.
DALL·E 1 Charateristics#
Controlling Attributes#

Drawing Multiple Objects#

Visualizing Perspective and Three-Dimensionality#

Visualizing Internal and External Structure#

Inferring Contextual Details#

DALL·E 1 Architecture#
The transformer is a large model with 12B parameters.
It consisted of 64 sparse transformer blocks with a complicated set of attention mechanisms inside, consisting of
classical text-to-text masked attention,
image-to-text attention, and
image-to-image sparse attention.
All three attention types are merged into a single attention operation.
The model was trained on a dataset of 250M image-text pairs.
VQ-VAE#
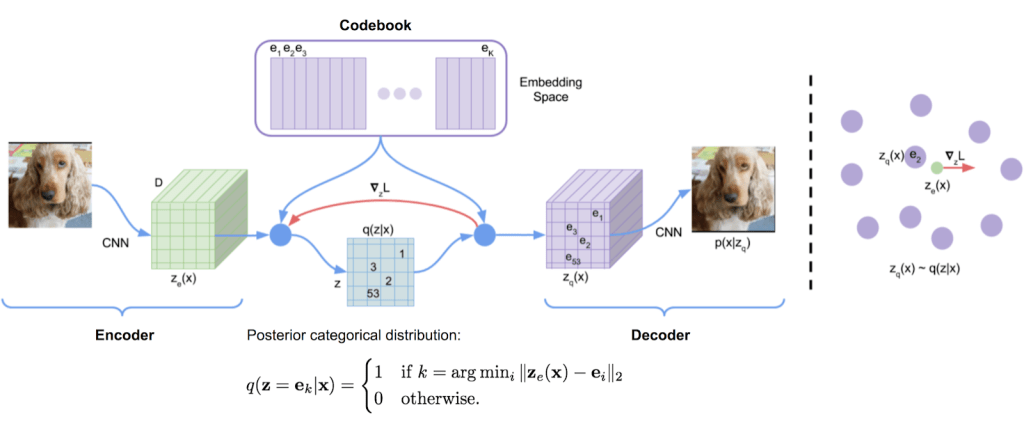
VQ-VAE is a type of variational autoencoder that uses vector quantization to obtain a discrete latent representation.
This is in contrast to the continuous latent space that other variational autoencoders have.
The objective function of a VQ-VAE, when trained on an image dataset, can be written as:
\(\mathcal{L} = \mathbb{E}_{q(z|x)}[\log p(x|z)] - \beta \cdot D_{KL}[q(z|x) || p(z)]\)
where \(p(x)\) is the data distribution, \(q\) is the approximate posterior over latent variables and \(D_{KL}\) denotes the Kullback-Leibler divergence.
This objective function encourages the model to learn an efficient codebook that minimises reconstruction error while also matching the prior distribution over codes.
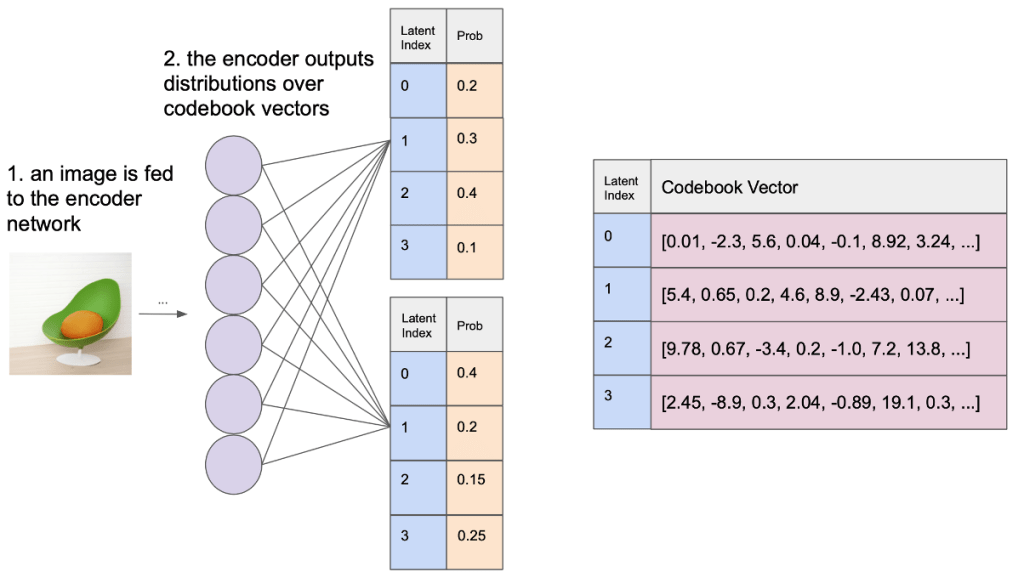
A latent space
A latent space is obtained by encoding the input image into the nearest codebook entry. This process is called vector quantization and results in a discrete latent space.
Autoencoders#
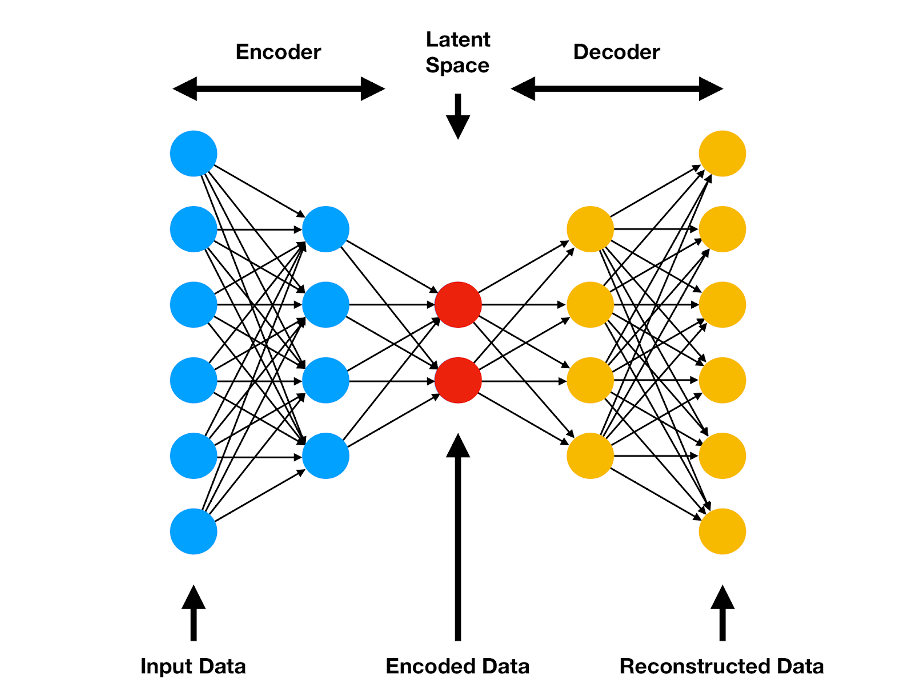
Autoencoder is a neural network that is trained to predict its input.
The objective function of an autoencoder can be written as:
\(\mathcal{L} = \mathbb{E}_{p(x)}[\log p(x|z)]\)
where \(p(x)\) is the data distribution and \(p(x|z)\) is the model distribution.
This objective function encourages the model to learn a latent space that captures the underlying structure of the data.
A VQ-VAE can be seen as a type of autoencoder where the latent space is constrained to be discrete.
Variational Autoencoders (VAE)#
Variational Autoencoders (VAE) is a type of autoencoder where the latent space is continuous.
The objective function of a VAE can be written as:
\(\mathcal{L} = \mathbb{E}_{q(z|x)}[\log p(x|z)] - D_{KL}[q(z|x) || p(z)]\)
where \(p(x)\) is the data distribution, \(q\) is the approximate posterior over latent variables and \(D_{KL}\) denotes the Kullback-Leibler divergence.
This objective function encourages the model to learn a latent space that captures the underlying structure of the data while also matching the prior distribution over latent variables.
Discrete Spaces#
Discrete spaces are more efficient to represent than continuous spaces.
This is because a discrete space can be represented with a finite number of bits, whereas a continuous space requires an infinite number of bits.
In addition, discrete spaces are easier to manipulate and reason about than continuous spaces.
For these reasons, VQ-VAE is more efficient than VAE at learning latent representations of data.
Uncertainty in the Posterior#
Uncertainty in the Posterior
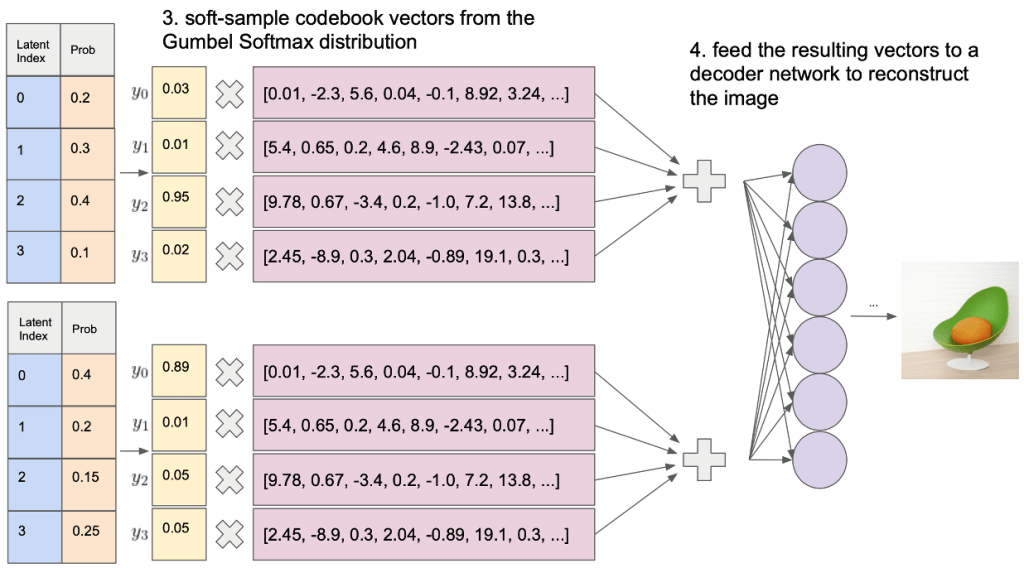
Uncertainty in the posterior is added by soft-sampling codebook vectors from the Gumbel-Softmax distribution.
This results in a softened latent space which can be seen as a continuous approximation of the discrete latent space.
The Gumbel-Softmax distribution is a type of distribution that allows for sampling from a discrete space while still allowing for gradients to flow through the samples.
This is useful for training models with discrete latent spaces, such as VQ-VAE.
The Gumbel-Softmax distribution is defined as:
\(G(z;\mu,\beta) = \frac{\exp((z - \mu)/\beta)}{\sum_{k=1}^K \exp((z_k - \mu)/\beta)}\)
where \(\mu\) is the mean, \(\beta\) is the temperature and \(K\) is the number of classes.
Comparison of original images (top) and reconstructions from the dVAE (bottom)

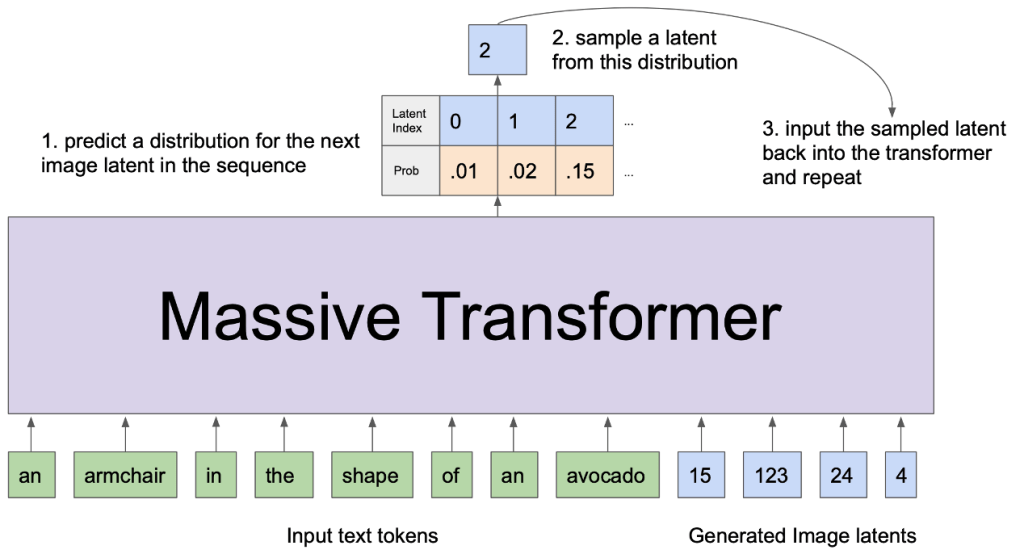
Decoder#
A GPT-3 like transformer decoder consumes a sequence of text tokens and (optional) image tokens (here a single image token with id 42) and produces a continuation of an image (here the next image token with id 1369)

Sampling From a Trained DALL-E#
DALL·E 1 Results#
Several image generation examples from the original paper

The trained model generated several samples (up to 512!) based on the text provided, then all these samples were ranked by a special model called CLIP, and the top-ranked one was chosen as the result of the model.


